3月3日はてらこやの日でした。社協さんからゴーフル他のお菓子のセットの差し入れいただきました。
小学生にはストロベリーのゴーフルが人気で、後から来る中学生への配分も考えるとどうやって分けたらいいかなかなか意見がまとまりません。でも、待てよ?そもそもゴーフル(大)1枚はゴーフル(小)何枚分なんでしょう?まずは直径を図って面積を計算してみることにしました。その後、中学生(予想出席者数)も含めての1人何枚ずつ分ければよいかを考えてみました。最終的には最初人気の集中したストロベリーが残ったりして。きっと、どんなお菓子があるか一つ一つよく吟味しているうちに「こっちの方がよさそう」なんて気が変わったのかもしれませんね。
中学生には小学生が分けてくれたお菓子を配給しました。出席者が3人で少し寂しいかったですが、確率の問題に挑戦したり、パソコンで調べものをしたりしました。パソコンでは最初はウクライナ侵攻について調べていたのですが、次第に伊豆急行の電車について検索していたり、ついつい興味のあることに熱中してしまいました。電車で旅行の計画って、時間とお金、それに乗りたい電車の種類まで考えると、色々な組み合わせから選択したり、意思決定する必要があるんですね。勉強になります。

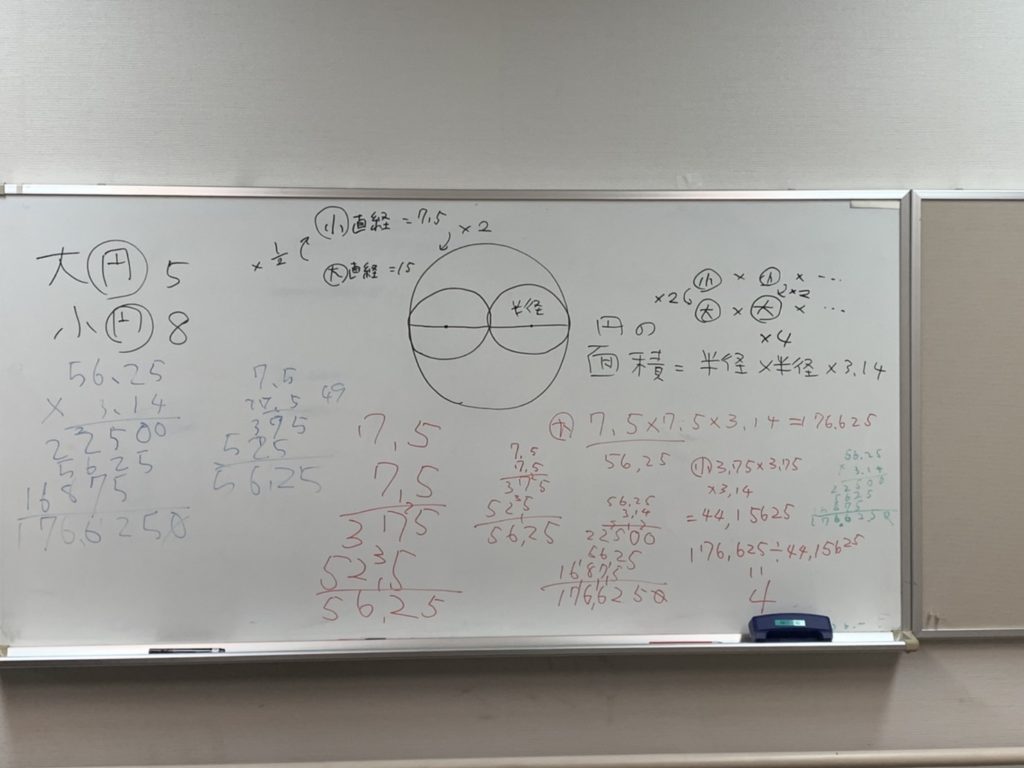
『具体と抽象』 大きいゴーフルの半径は小さいゴーフルの2倍ありました。では面積は何倍になる? 「円の面積は半径✖半径✖3.14」 2倍✖2倍✖3.14で答えは4倍。(ちなみに、半径が3倍だったら9倍)本当に4倍になるのか小さいゴーフルの面積を4倍にして大きいゴーフルの面積になるのか確かめている子がいました(素晴らしい!)実感が伴う具体的な経験がとても大事です。中学の数学になると文字式や関数など、いきなり抽象度が上がります。そこで大切になってくることは、小さい時から、遊びや生活の中で具体的な数や量、距離などの感覚を経験すること。その経験値があって、抽象度をあげていくことが大切。だからこそおぎゃぁと生まれた時から子供は、自然に触れ、いっぱい遊ぶことが最大の勉強になるのです。誰よりも早く計算ができるようになるより、漢字をたくさん覚えるよりも…